本文包含原理图、PCB、源代码、封装库、中英文PDF等资源
您需要 登录 才可以下载或查看,没有账号?注册会员
×
摘 要: 关键词: MIMO-OFDM;信道估计;空频域导频;保护频带
正交频分复用OFDM(Orthogonal Frequency Division Multiplexing)技术是一种多载波数字调制技术[1]。它具有极好的抗多径能力和极高的频谱利用率,因此被广泛应用于数字宽带通信领域。多天线技术MIMO(Multiple Input and Multiple Output)充分利用空间资源, 在收发端实现多发多收, 在不增加频谱资源和天线发送功率的情况下, 能有效提高信道容量。两种技术的联合--MIMO-OFDM 技术作为下一代无线通信系统的核心技术近年来引起了众多相关研究者的研究兴趣。
MIMO-OFDM系统中,为了在接收端准确地恢复发送端所发送的原始信号,需要得到有效的信道信息,因此信道估计是MIMO-OFDM系统的关键环节。目前基于空时域导频结构的信道估计方法[2-4]是研究的主要方向。为了保证最小二乘LS(Least Square)信道估计的均方误差MSE(Mean Square Error)最小,需要频带中每个导频的能量均相等,每根发射天线中的导频等间隔放置,而且不同发射天线中的导频序列相互位置正交[4],即在其中一根发射天线传输导频时,其他发射天线导频位置的子载波不被使用。可见,基于这种导频结构的信道估计需要信道状态至少在两个OFDM符号的传输过程中保持不变。而在参考文献[5]中,提出了一种基于空频域的导频结构,相对于基于空时域导频结构而言,这种导频结构的主要优势在于,不同发射天线可以同时传输导频信息,更重要的是,在一个OFDM符号内便可以进行信道估计。结果表明,在相同的仿真条件下,基于空频域导频信道估计的MIMO-OFDM系统在性能上有了明显改善。
为了在基于空频域导频结构的MIMO-OFDM系统中,使LS信道估计得到最小MSE,本文研究了此导频结构所允许的极限保护频带宽度以及最佳初始导频位置[6]。通过设置OFDM的保护频带宽度和调整初始导频位置来避免部分导频信号落入保护频带中,从而避免了传输数据受到发送端低通滤波器的失真影响,改善了系统性能。
1 MIMO-OFDM系统模型
如图1所示MIMO-OFDM系统中有NT根发送天线和NR根接收天线。数据流经过空时编码和空时复用发送到各个天线。每根天线上的频域数据经过K点IFFT变换为时域数据加入循环前缀发送到信道中。在接收端去除循环前缀并对时域采样值进行FFT变换,同时将导频和数据符号分离出来,导频符号用做信道估计,得到的信道估计矩阵可以帮助MIMO解码器更为精确地解调出OFDM符号。
假设接收天线与发射天线之间的信道都是相互独立的,则第j根接收天线上第n个OFDM符号的第k个子载波上的接收信号可表示为:

2 最优空频导频结构设计与信道估计
参考文献[5]提出了一种基于空频域的导频结构(导频结构如图2所示),在相同的仿真条件下,相对于基于空时域的导频结构而言,此种新颖的导频结构在MIMO-OFDM系统的信道估计问题上有着明显的优势:(1)在一个OFDM符号传送时间内就能够进行信道估计,而基于空时导频结构的信道估计至少需要完成两个OFDM符号的传输才能进行。因此这种导频结构更能胜任快衰落信道的信道估计。(2)由参考文献[5]的仿真结果图可知,基于空频域导频信道估计的MIMO-OFDM系统在性能上相对于基于空时域导频信道估计的MIMO-OFDM系统有着明显的改善。

本文以一个2发2收的MIMO-OFDM系统为例,设置导频值为:


图3显示了OFDM符号的子载波与保护频带,当导频子载波不落入保护频带之内时,MIMO-OFDM系统即能避免传输信号受到发送端低通滤波器的失真影响,也能保证XXT为对角矩阵,从而进一步保证了最小二乘信道估计的均方误差最小。相反,导频子载波落入保护频带内,由于滤波器的影响,XXT将变成非对角矩阵,此时系统将无法得到最佳性能。

针对基于空频域的导频结构,计算OFDM系统存在的极限保护频带宽度。

同时,提出一种基于空时域的导频结构(如图4)作为参照,分别观察两种导频结构,在保护频带大于极限保护频带宽度和小于等于极限保护频带宽度两种情况下的性能。
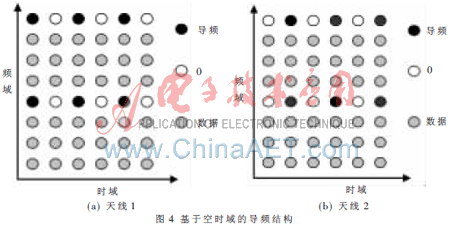
根据基于空时域的导频结构,可以设其导频序列的初始点为do,导频序列的终点为dp-1=do+(P-1)V。
为了使初始导频和终点导频避开保护频带,do、dp-1同样需满足式(6)的条件,再结合dp-1=do+(P-1)V,可以得到do的取值范围是:

3 仿真结果与结论
基于以上分析,建立了MIMO-OFDM系统的仿真平台。此系统采用2根发射天线和2根接收天线,512个子载波,信道采用多径瑞利信道,信道长度L=8,多普勒频移fd=50,系统采用QPSK调制和STBC编码。由式(9)和式(12)可以计算出两种导频结构的极限保护频带宽度都为。
图5给出了保护频带宽度都为31,初始导频位置都为32时,基于空时域导频结构的MIMO-OFDM系统和基于空频域导频结构的MIMO-OFDM系统的性能曲线。从仿真结果图可得,采用空频域导频结构的MIMO-OFDM系统在性能上有着明显的改善。
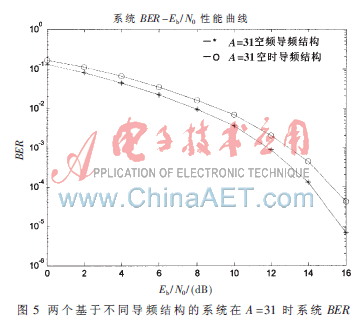
图6、图7分别给出了当保护频带分别为31和60时,基于空频域导频结构的MIMO-OFDM系统和基于空时域导频结构的MIMO-OFDM系统的性能曲线。从仿真结果得知,当保护频带A为60,大于极限保护频带宽度,初始导频位置为61时,最终的导频位置落入保护频带内,导致系统误差增大。当保护频带A为31,等于极限保护频带宽度,初始导频位置为32时,防止了导频子载波落入保护频带内,保证了LS信道估计的MSE最小,性能达到最优。
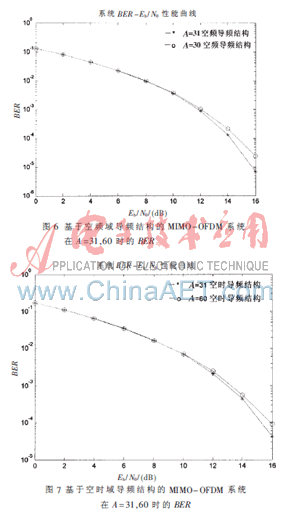
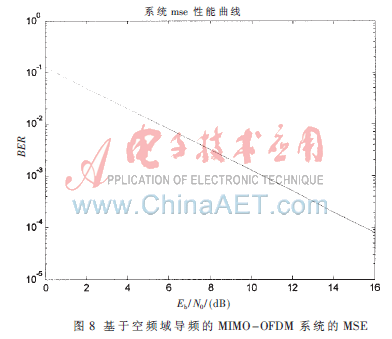
图8显示了采用空频域导频结构的MIMO-OFDM系统的均方误差(MSE)。
本文进一步证实了采用空频域导频结构的MIMO-OFDM系统在性能上相对于基于空时域导频结构的MIMO-OFDM系统有着明显的改善。
在基于空频域导频信道估计方法的MIMO-OFDM系统中,保护频带宽度小于或等于极限保护频带宽度时,选择最佳的初始导频位置,可以保证LS信道估计的MSE最小,从而能得到系统的最优性能。
参考文献
[1] 王文博, 郑侃编着.宽带无线通信OFDM技术[M]. 北京: 人民邮电出版社,2003.
[2] 胡蝶,何良华.一种改进的MIMO-OFDM系统导频设计方案[J].电子与信息学报, 2009, 31(4).870-873.
[3] LI Y, SESHADRI N, ARIYAVISITAKUL S. Channel estimation for OFDM systems with transmitter diversity in mobile wireless channels[J]. IEEE Journal on Selected Areas in Communications,1999,17(3):461-471.
[4] BARHUMI I, LEUS G, MOONEN M. Optimal training design for MIMO OFDM systems in mobile wireless channels[J]. IEEE Transactions on signal processing, 2003,5(7):1615-1624.
[5] PEI Sheng P, BAO Yu Z.Channel estimation in space and frequency domain for MIMO-OFDM systems [J]. The Journal of China Universities of stsand Telecommunications, 2009, 16(3):40-44.
[6] 王晗, 汪晋宽. MIMO-OFDM系统信道估计中的最优导频设计[J].电波科学学报,2008,23(3):501-505. |
 |手机版|MCU资讯论坛
( 京ICP备18035221号-2 )|网站地图
|手机版|MCU资讯论坛
( 京ICP备18035221号-2 )|网站地图