基于核主量和线性鉴别分析的人脸识别算法研究

摘 要：  关键词： PCA; LDA; KPCA; 核函数； 欧氏距离分类； ORL人脸库
       近些年,人脸识别已成为计算机视觉和模式识别领域中的热门课题，有着广阔的应用前景。众所周知，人脸识别是典型的高维数据分类问题，即人脸的原始特征对应高维空间中矩阵数据的图像，然而在人脸识别中直接应用这些数据会使计算速度明显降低，不利于现代科学领域对人脸识别速度和精度的要求。现今人脸识别领域中面临的问题是提取什么样的特征利于分类器的分类以及如何减少高维数据的运算等。迄今为止，线性子空间方法在特征提取中得到了广泛的发展，其中主成分分析(PCA)[1]和线性鉴别分析(LDA)[2]方法是人脸识别中广为采用的基本方法。尽管这些子空间方法在人脸识别中得到了比较成功的应用，但人脸表观由于受外在和内在因素的影响，如脸部表情、脸部姿态(或照相机视角)、光照以及人脸形状和皮肤的反射特性等，人脸空间更可能存在于非线性子空间上。
     近十年来，核函数技术在模式识别领域中得到了迅猛的发展。SCHFILKOPF 等利用核技术将经典的主分量分析(PCA)推广到核主分量分析(KPCA) [3],实验结果表明，KPCA不仅能够抽取非线性特征，而且具有更优的识别结果。
     受KPCA的启发，本文首先采用KPCA方法，将高维图像投影到低维的子空间中，然后在子空间中进一步采用基于主元空间的线性鉴别分析（LDA）和欧氏距离最近邻分类(KNN)相结合的方法，有效地利用了人脸的非线性信息，同时两次投影之后，提高了计算机的识别速率和准确率。
1主成分分析方法的实现
1.1基本PCA方法
     PCA的主要思想是寻找一组单位正交向量基，用其线性组合重构原样本，使得重构后的样本和原样本的均方误差最小[4]。在实际计算中，通过求取样本投影之后的协方差矩阵的特征值和特征向量对样本进行描述，以达到降低特征空间维数的目的，具体如下：


     这样Y就是X经PCA变换后得到的特征子空间,达到将训练样本从高维空间降到低维子空间的目的。
1.2 KPCA方法的实现
　PCA是最基本的无监督线性子空间降维方法，且由上述可知，PCA通过选取最优特征向量基Wr获得最佳投影子空间。但PCA是线性方法，只能揭示人脸图像中的线性信息，忽略了数据中的非线性信息。20世纪90年代以来，基于核的非线性特征提取法得到了发展，该方法有效地利用了人脸图像的非线性信息[5]。本文通过核映射将样本数据映射到核空间中，然后在核空间中运用PCA法对高维空间中的人脸信息进行非线性操作，进而投影到线性低维子空间中。该方法称为核主成分分析法,即KPCA。具体方法如下：

   
   

3 算法描述
     本文采用Matlab仿真工具对算法进行仿真，验证各算法的实现效果。训练样本和测试样本均采用ORL人脸库，该库由40人组成，每人由10幅112×92的图像组成 。具体算法实现过程如图1所示。
   
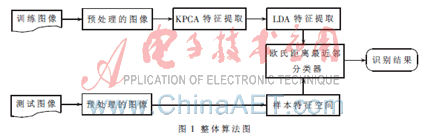
       (1) 读入ORL人脸库图像，为了提高运算速度，降低图像维数，适当调节图片大小。随机选取每人的5幅图像作为训练样本，其余的5幅图像作为测试样本。即200幅训练样本图像，200幅测试样本图像。

   
4 实验结果分析
4.1核空间参数的选取
     核参数α的选取及实现结果如表1所示。
   
   
4.2 Matlab仿真效果图
     (1)利用KPCA对训练样本图像首次投影后得到的特征脸如图2所示。
   
       (2) 采用LDA再次降维并用KNN分类，最终得到的识别对比效果图如3所示。
4.3 各种算法的对比
     本文在ORL人脸库下，应用Matlab分别验证了基本PCA、主元空间LDA、PCA+LDA、KPCA、KPCA+LDA以及KPCA+LDA+KNN等算法的识别率、投影向量个数、训练时间、测试时间等各项指标,具体结果如表2所示。
   
   
     由表2可以看出，采用基于KPCA+LDA+KNN算法的人脸识别率和其他各项指标皆明显高于其余五种方法，这主要是因为采用KPCA可以更好地分析图像空间中的非线性关系，比起只采用线性PCA和线性LDA方法明显减少了人脸高维空间中信息的丢失。同时利用基于主元空间LDA的方法，加之KNN最近邻分类器的使用,有效地降低了投影向量个数，加快了计算速度。
     本文提出的KPCA+LDA+KNN算法中,不但采用了非线性子空间降维方法，同时采用了基于主元空间LDA的方法，加之融入欧氏距离最近邻分类器的方法，从而改善了人脸识别的效果。本文提出的算法不仅能够使高度复杂和非线性的原始样本线性化、简单化， 而且能够使样本特征之间的冗余信息明显降低，防止有用信息的丢失[9]。最后本文在ORL人脸库下，应用Matlab验证了该算法的有效性，但是不同核函数的选取以及不同分类器的使用对提高该算法的识别性是否有效，有待于进一步的研究[10]。
参考文献
[1] BATUR A U, HAYES M H I. Linear subspaces for illumi2 nation robust face recognition[A]. Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition[C].2001,02:296-301.
[2] SHAKUNAGA T,SHIGENARI K.Decomposed eigenface for  face recognition under various lighting conditions[A]. Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition [C].2001,01(1):864-871.
[3] LIU C J, HARRY W. Enhanced fisher linear discriminant models for face recognition.140Inter.ConL on Pattern Reco  gnition.ICPR’98,Queensland,ustralia'V01.II,PP[M].1998: 1368-1372.
[4] 钟向阳,胡仕明.基于主分量线性判别方法人脸识别系统的实现[J].嘉应学院学报(自然科学),2006,24(3):832-887.
[5] SEHOLKOPF B, SMOLA A, MULLER K R.Kernel principal component analysis[A].In:W.Gerstner,edi:Proceedings of International Conference on Artificial Neural Networks  Lecture Notes in Computer Science[C]. Berlin:Springer,1997, 1327:583-588.  
[6] ROTH V,STEINHAGE V. Nonlinear diseriminant analysis using kernel functions[A]. In:Solla S A,Leen T K,Muller K.R, editors.Advance in Neural information Processing Systems 12[C]. Cambridge,MA,USA: MIT Press,2000:568-574.
[7] CHEN L, IIAO H, KOM,et a1. Anew LDA based face recognition system which can solve the small sample size problem[J]. Pattern Recognition,2000,(33):1713-1726.
[8] YANG Jian, FRANGI A F, YANG Jing Yu, et a1. KPCA Plus LDA: acomplete kernel fisher discriminant framework for feature extraction and recognition[J].IEEE Transactions on Pattern Analysis Machine Intelligence, 2005,27 (2):230-244.  
[9] 王婷,杨国胜,薛长松.若干人脸识别算法的比较研究[J].河南大学学报(自然科学版),2007,37(2):192-194.
[10] GUNTURK B K, BATUR A U, ALTUNBASAK Y, et al. Eigenface-based super-resolution for face recognition [A]. Proceedings.International Conference on Image Processing[C].2002,(2):845-848.