基于Verilog HDL设计实现的乘法器性能研究

摘要：

   关键词：Verilog HDL；改进Booth算法；乘法器；
   1 引言
        Verilog HDL是当今最为流行的一种硬件描述语言，完整的Verilog HDL足以对最复杂的芯片和完整的电子系统进行描述[1]。本文采用Verilog HDL语言来设计实现4-2和5-2混合压缩器构成的乘法器的设计，并与另外实现的两种乘法器从速度，面积和硬件资源占用率等方面进行了性能比较，得出用这种改进压缩器要比两位阵列乘法器和传统的4-2压缩器构成的乘法器速度提高了10％，硬件资源占用减少了2％。
   2 两位阵列乘法器
   阵 列乘法器基于移位与求和算法。两位阵列乘法器是对乘数以2bit进行判断，这样可以在部分积的数目上比一位判断阵列乘法器减少1倍；另外，阵列乘法器结构 比较规范，利于布局布线，但是阵列乘法器存在进位问题，运算速度比较慢，所需时钟周期长，时延大。以下是两位判断的乘法器的Verilog HDL语言部分程序：
   module imult _radix_2(prod,ready,multiplicand,multiplier,start,clk);
         ……
           case ( {product[1:0]} )
             2'd0: pp = {2'b0, product[31:16] };
             2'd1: pp = {2'b0, product[31:16] } + multiplicandX_1;
             2'd2: pp = {2'b0, product[31:16] } + multiplicandX_2;
             2'd3: pp = {2'b0, product[31:16] } + multiplicandX_3;
           ……   
   3  改进Booth编码乘法器
          阵列乘法器虽然占用相对较少的硬件面积，可是运算速度非常慢，不能满足高速运算的要求。为了得到高速的乘法器，可以从两个方面来提高乘法器的计算速度：减 少部分积数目；提高部分积压缩速度。通常减少部分积数目采用二阶的Booth编码实现；可用4-2压缩器构成的Wallace树来提高部分积求和速度。本 文采用4-2压缩器和5-2压缩器的混合Wallace树来进一步提高求和速度。www.51kaifa.com
          改进Booth算法通过对二进制补码数据重新编码，压缩PP（部分积）数目，以提高运算速度。其中，压缩率取决于编码方法，如果采用三位编码，可压缩 1/2的PP，再对所得的n/2个部分积进行求和运算。在电路实现中还可采用混合握手协议和管道传输方式，可以降低电路的功耗，仅占Amulet3i乘法 器的每次运算的能量消耗的50％【2】，另外，也可以采用混合逻辑乘法器设计【3】。Booth算法电路图在文献[4]中有具体介绍。
   3.1  4-2压缩器
           4-2压缩器使用2个CSA（Carry-save Adders保留进位加法器），将5个数据（4个实际数据和一个进位）相加产生3个数（Sun, Carry和Cout）。4-2压缩器结构图如图1所示【4】。
   
   
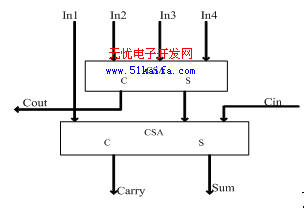
   图1 由2个CSA构成的4-2压缩器
           4-2压缩器是进行部分积压缩最常用到的部件，与全加器相比，具有电路简单、连线规则的优点．传统4-2压缩器输入与输出的逻辑关系表达式[8]为：www.51kaifa.com
   
          表达式中：In1～In4为部分积输入信号；Cin为邻近压缩器进位输入；Sum为伪和；Carry和Cout为进位输出,其权值相同。由图及表达式知， 输出进位与输入进位式相互独立的，即输出并不由输入产生，这样就能保证部分积同时且独立地相加。4-2压缩器对部分积进行压缩的图如图2【5】所示：
           
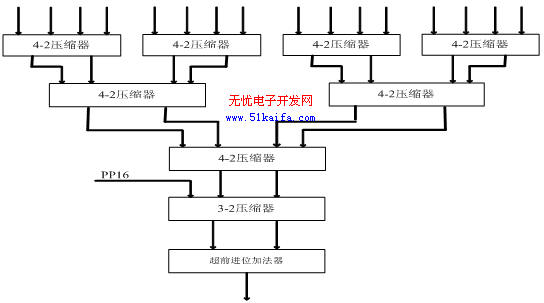
                     图2  4-2压缩器组结构图
          由4-2压缩器进行部分积压缩的Booth乘法器的Verilog HDL描述部分程序如下：
   module Booth_radix_4(prod,ready,multiplicand,multiplier,start,clk);
        ……  
         dug dug0(PP0,mult[2:0]);
               ……
   count count1(clock,sum0,carry0,PP0,PP1,PP2,PP3,cout0,cin0);
        count count2(clock,sum1,carry1,PP4,PP5,PP6,PP7,cout1,cout0);
         ……
        count count3(clock,sum,carry,sum0,carry0,sum1,carry1,cout,cin0);www.51kaifa.com
          ……
   3.2    4-2和5-2混合压缩器
        4-2压缩器在很大程度上减少了部分积的求和速度，但是它有一个缺点是Sum（伪和信号）比Carry（进位信号）的产生速度慢，因此，进位信号必须等待伪和信号的产生，这样又造成了压缩速度的降低和功耗的增加．可以用异或门和2-1数据选择器对电路进行变换【6】，这种结构能同时产生伪和信号和进位信号，并且关键路径的延迟也只有全加器的1.5倍【8】。为进一步压缩部分积的求和级数，加快压缩速度，本文同时采用了4-2压缩器和5-2压缩器混合逻辑设计。5-2压缩器的结构图如图3【7】所示，
   
   
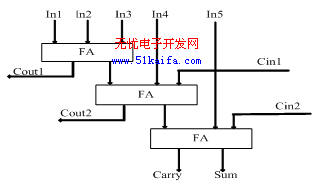
   图3  5-2压缩器的结构图
           5-2 压缩器有7个输入In1~In5（权值相同）,3个进位输出（权值相同）和一个伪和（权值比进位输出低一位），这种结构的压缩器结构规整，且仅有6个异或 门的延迟。文献[8]中给出了5-2压缩器的输入与输出的逻辑关系表达式。整个压缩器结构图如图4所示：
   
   
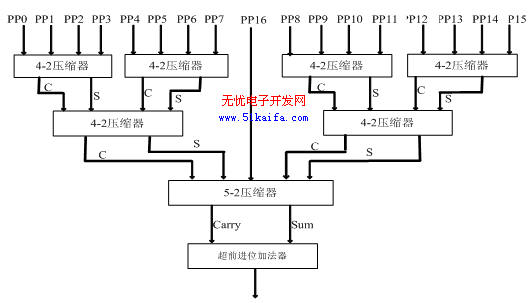
                 图4  本文采用的整个压缩器结构
          由4-2和5-2混合压缩器实现的改进Booth乘法器的Verilog HDL描述部分程序如下：
   module Booth_radix_5(prod,ready,multiplicand,multiplier,start,clk);
        ……  
         dug dug0(PP0,mult[2:0]);
         dug dug1(PP1,mult[4:2]);
         ……
   count count1(clock,sum0,carry0,PP0,PP1,PP2,PP3,cout0,cin0);
              ……
         sum sum1(clock,sum,carry,In16,sum0,carry0,sum1,carry1,cout,cin0,cin1);
          ……
   4逻辑仿真及性能比较
         本文在Xilinx ISE和Quartus II两种集成开发环境下， 对以上3种结构的乘法器进行了编译、综合、适配、时序仿真以及功率分析，其中输入信号的字宽为32bit。有仿真工具Xilinx ISE和Quartus II进行的仿真结果报告文件，很容易做出对这3种乘法器的性能比较，如表1所示。
   表1  3种乘法器性能比较表

Resources Summary
乘法器类型	资源占用率	面积（mm2）	时延（ns）
两位阵列乘法器	37/128(29%)	6.91	8.285
4-2压缩的Booth乘法器	38/256(15%)	12.07	3.99
4-2和5-2混合压缩的             Booth乘法器	35/256(14%)	11.849	3.59

         有性能比较表知：阵列乘法器面积最小，功耗小，但是运行速度慢；单纯使用4-2压缩器的Booth乘法器在资源占用率和速度上要比阵列乘法器提高约1倍， 功耗略大于阵列乘法器；而本文设计采用的乘法器方案有效提高了乘法器的运算能力，应用在FPGA上工作频率可达256.61MHz，要比传统的4-2压缩 器构成的乘法器在速度上提高了10％，硬件资源占用减少了约1％。
   4结论
          不同架构的乘法器在性能上都存在优点和缺点，在选择乘法器时，应根据应用场合的要求在速度、面积和功耗等方面综合考虑，本文采用Xilinx ISE和Quartus II两种集成开发环境对所实现的乘法器综合进行测试，更能准确显示不同结构的乘法器的性能优势，帮助用户快速选择合适的乘法器。本文设计采用的乘法器方案要比传统的4-2压缩器构成的乘法器在速度上提高了10％，硬件资源占用减少了约1％，有效提高了乘法器的运算能力。
            本文作者创新点: 本文采用4-2和5-2混合压缩器对部分积进行压缩，减少了乘法器的延时和资源占用率；并用Verilog HDL语言实现了两位阵列乘法器和传统的Booth编码乘法器。同时在Xilinx ISE和Quartus II两种集成开发环境下进行综合仿真测试，这更有利于比较乘法器的性能优势，便于用户更准确地选择适合应用场合的乘法器。
   
   参考文献：
   [1]王冠,黄熙,王鹰.Verilog HDL与数字电路设计[M].北京:机械工业出版社,2006
   [2]Yijun Liu.An Asynchronous Pipelined 32×32-bit Iterative Multiplier Using Hybrid Handshaking Protocol.http://async.org.uk/ukasyncforum14/forum14-papers/forum14-liu. pdf
   [3]何静,李清峰.基于CPLD的混合逻辑乘法器的设计[J].微计算机信息,2006,22(17):244-246.www.51kaifa.com
   [4]Dony C,Purchase J.Winder R.Exception Handling in Object-oriented System[C].Report on ECOOP91 Workshop W4,1991:17-30.
   [5] 王新刚,樊晓桠,李瑛,等.一种并行乘法器的设计与实现[J].计算机应用研究,2004,(7):135-137.
   [6] Radhakrishnan D,Preethy A P. Low power CMOS pass logic 4-2 compressor for high-speed multiplications[c]∥Proceedings of the 43rd IEEE Midwest Symposium of Circuits and Systems. Piscataway,USA:IEEE,2000:1296
   -1298.
   [7] Pallavi Devi Gopineedi, Himanshu Thapliyal, M.B Srinivas, Hamid R. Arabnia. Novel and Efficient 4: 2 and 5: 2 Compressors with Minimum Number of Transistors Designed for Low-Power Operations,ESA,2006: 160-168.
   [8]梁峰,邵志标,梁晋.Radix-16 Booth流水线乘法器的设计[J].西安交通大学学报,2006,40(10):1111-1114.