基于FIOS类型的Montgomery双域模乘器设计

摘  要： 针对FIOS类型的Montgomery模乘扩展算法的比特级-字级和字级-字级的两种实现形式进行研究，设计多处理单元的流水线组织结构实现算法，并对模乘器进行双有限域统一结构设计，使之能够同时支持两个有限域GF(p)和GF(2n)上的运算。最后对设计的两种模乘器用Verilog硬件描述语言进行代码描述,采用Synopsys公司的Design Compiler 在Artisan SIMC 0.18 μm typical工艺库下综合。实验结果表明，该模乘器不仅在运算速度和电路面积方面各具有优势，而且具有运算长度可变的灵活性。
关键词： 椭圆曲线加密算法； Montgomery模乘器； 比特级-字级算法； 字级-字级算法
       随着计算机网络的发展和普及，信息安全问题越来越多地被人们所关注。公钥密码体制有效地解决了在公共信道上保护信息的抗抵赖性、身份认证、密钥分发等问题。椭圆曲线密码ECC（Elliptic Curve Cryptography）是一种基于椭圆曲线离散对数问题的公钥密码，1985年分别由Miller [1]和Koblitz[2]独立提出。相对于其他公钥密码系统，椭圆曲线密码系统具有计算速度快、存储空间小、带宽要求低等优点，特别适用于各种无线设备和智能卡等计算资源受限的设备，因而受到了人们的广泛关注，成为新一代公钥密码标准。而模乘运算是椭圆曲线加密算法中的核心运算，如何高效地实现模乘运算是当前的一个研究热点。
     Montgomery模乘算法[3]是目前应用最为广泛、同时也是最为高效的模乘算法。但Montgomery模乘算法存在的主要问题是模乘运算数据长度固定，不具备可配置性。另一个缺陷就是模乘运算的数据路径延迟达到2级n位全加器的延迟，极大地限制了电路的时钟频率。Bajard将Montgomery模乘算法扩展到剩余数系统RNS(Residue Number System),并进一步提高了模乘的性能，但数系转换硬件实现复杂，并且不支持双域运算[4]。在对算法进行硬件实现时，一般是将运算数据分成若干个字，对运算数据按字进行处理，以提高算法并行度和电路时钟频率，参考文献[5]提出了基于高基阵列的Montgomery模乘算法。
     目前Montgomery模乘运算的扩展和优化实现算法主要可以分为以下四种类型：比特级-完全长度BLFP(Bit-Level Full-Precision)算法；比特级-字级BLWL(Bit-Level Word-Level)算法；字级-完全长度WLFP(Word-Level Full-Precision)算法，对另一个运算数据按完全长度进行处理；字级-字级WLWL(Word-Level Word-Level)算法。因为BLFP和WLFP类型的算法与原始Montgomery模乘算法存在相同的缺陷，所以考虑到设计高效的模乘运算单元，本文基于BLWL和WLWL这两种类型的算法,结合FIOS(Finely Integrated Operand Scanning) Montgomery模乘扩展算法，提出了一种Montgomery双域模乘器实现方案。结果表明,相比较于传统的Montgomery模乘器，本文的设计减少了近一半的时钟周期数，不仅大大提高了模乘运算速度，而且支持运算长度可配置的两个有限域GF(p)和GF(2n)的模乘运算，提高了模乘处理的灵活性。
1 FIOS类型的Montgomery模乘算法
     Montgomery模乘算法按求乘法部分积与约简运算结合方式的不同，参考文献[6]提出了SOS(Separated Operand Scanning)、CIOS(Coarsely Integrated Operand Scanning)、FIOS(Finely Integrated Operand Scanning)、FIPS(Finely Integrated Product Scanning)、CIHS(Coarsely Integrated Hybrid Scanning)这五种不同类型的Montgomery扩展算法，算法详细内容可参阅文献。
     五种算法中,在不考虑并行实现算法的前提下，FIOS算法的运算量最少。
1.1 BLWL类型的FIOS算法
     为缩短电路数据路径中的延迟，首先将BLWL类型的FIOS算法中的中间变量全部采用TS-TC这样的冗余数表示,以进位保留加法运算完成算法中的加法运算。在算法中以这样的形式表示进位保留加法(TC,TS)=X+Y+Z。算法中Ai表示A的第i 位， B(i)表示B的第i个字，运算数据字长为w bit，字数为s=「n/w?骎，该算法描述如下：
         

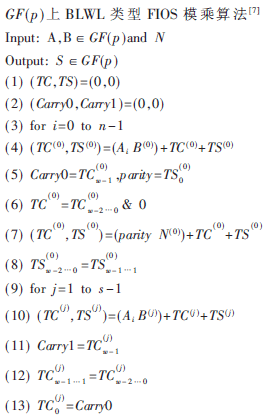
2 两种算法的流水线组织结构分析
2.1 BLWL类型算法的流水线组织结构
     通过对算法1的分析研究，可以采用多处理单元 的流水线结构来实现算法。流水线运算流程如图1所示，每一竖列表示一级流水线，每一横行表示一个运算周期，其中X和Y为运算处理单元。从图1可以看出，在外部循环i=0和内部j=1这两个过程经两个时钟周期完成后，才能够得到下一级流水线处理单元PU所需的(C(0)，S(0))，即此时才开始对A的第2个bit进行扫描。也就是说在第i个外部循环的第1个内部循环经两个时钟周期完成后才可以开始第i+1个外部循环的运算，所以采用这种流水线组织形式，每级流水线之间的延迟为两个时钟周期。因为流水线每级间存在两个时钟周期的延迟，所以需要两级寄存器用来存储中间结果，而且这种流水线组织形式会增加时钟周期数,降低运算速度。